Concrete Screw Anchors as Retrofit Anchor Bolts
Last updated November 30, 2024
By Ian Story
This post examines using Concrete Screw Anchors (such as the Simpson Titen HD concrete screw) as a replacement for cast in place anchor bolts in retrofit situations.
The IBC includes special provisions for cast in place anchor bolts with at least 7 inches of embedment (among other criteria). See 2021 IBC 1905.1.8 Exception 1. For anchors meeting these requirements, testing has shown that the bolted wood connection at the wall base plate fails before the concrete connection, so these anchors can be designed solely using NDS bolting criteria.
For anchors that do not meet the exception, the concrete strength needs to be evaluated. Whether the anchors need to be designed for overstrength is debatable. The relevant code section is ACI 318-19 17.10.6.3. It could be argued that the wood plate bearing on the anchor bolts provides a force-limiting mechanism, as discussed in the commentary for this code section. This appears to be the mechanism driving the IBC exception for anchor bolts. Because testing did not extend to concrete screws with short embedment lengths, we will conservatively assume for this article that this force-limiting mechanism cannot be relied upon, and we will design our connection assuming overstrength loading.
For the following calculations, we will use a setup as follows: 2,500 psi concrete, cracked, with no supplementary reinforcement. The concrete screws will be located in a 6 inch thick stem wall, with a minimum 2″ edge distance. The end distance is large enough that concrete breakout perpendicular to the applied force does not control. This leaves us with three potential failure modes at the concrete-steel interface: shearing of the concrete screws, pryout, and concrete breakout along the parallel edge. The calculations will be based on ACI 318-19 Chapter 17.
The basic concrete breakout strength is (ACI 318-19 Eq. 17.7.2.2.1a):
![]()
This is then modified by an area ratio, ![]() , where
, where ![]() is the full breakout cone area of a single anchor unconstrained by geometry, and
is the full breakout cone area of a single anchor unconstrained by geometry, and ![]() is the combined breakout cone area of all the anchors, taking into account overlaps and geometric constraints such as edge length. The number of anchors in the group is not explicitly considered, as this is baked into
is the combined breakout cone area of all the anchors, taking into account overlaps and geometric constraints such as edge length. The number of anchors in the group is not explicitly considered, as this is baked into ![]() .
.
For an anchor in shear, the full concrete breakout cone is:
![]()
For an infinite line of anchors, the effective concrete breakout cone is the smaller of the following:
![]()
![]()
This total is then modified by several other factors, including a strength reduction factor, but none of these factors will be influenced by the spacing or geometry of the connection at this scale. So for now we can focus on the above equations, and apply the remaining factors at the end.
First observation: for a given edge distance, the greatest capacity per screw occurs when the spacing, ![]() is greater than 3 times the edge distance,
is greater than 3 times the edge distance, ![]() . Adding screws at a spacing tighter than this reduces the capacity per screw, with no change to the total capacity of the system.
. Adding screws at a spacing tighter than this reduces the capacity per screw, with no change to the total capacity of the system.
Second observation: embedment length and anchor diameter both have a moderate effect on concrete breakout capacity, per the following chart (note: the leveling off at the top of the 3/4″ screw data is due to a limiting min() factor in the basic breakout strength equation that was omitted above, for conciseness).
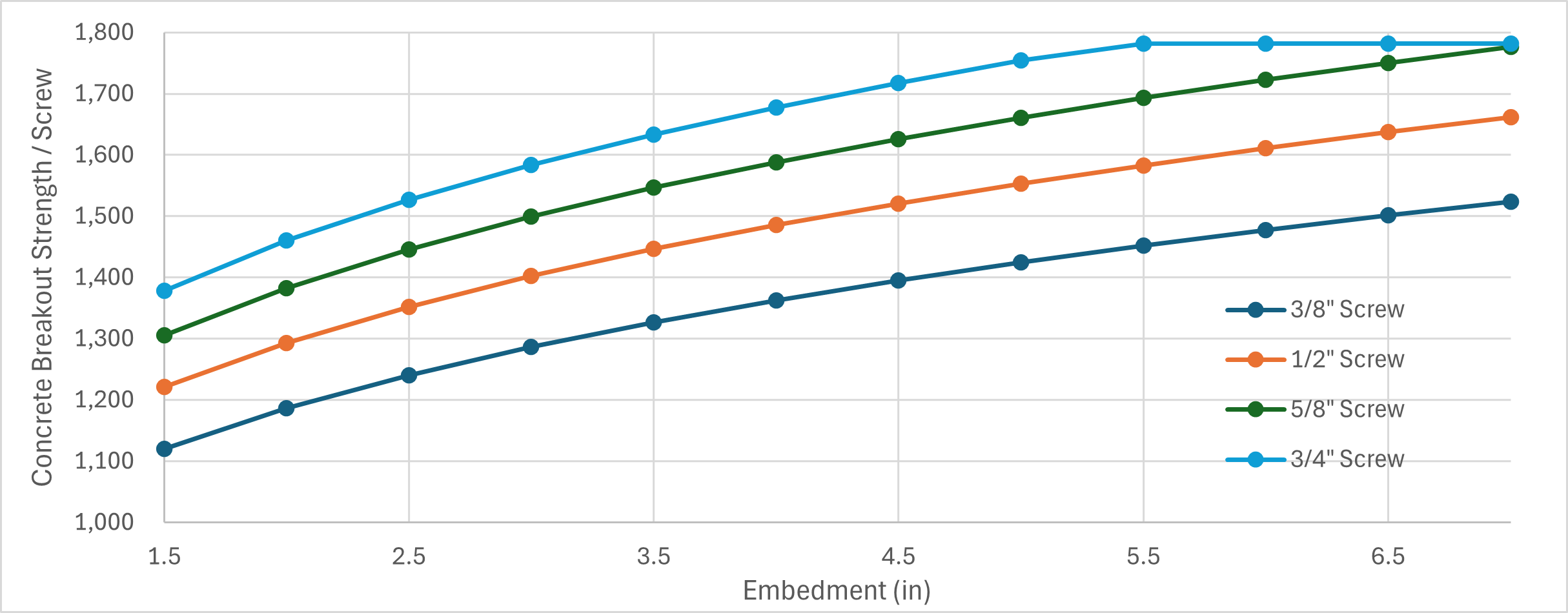
Final observation: the edge distance, ![]() is by far the largest lever we can pull to influence the strength of the connection.
is by far the largest lever we can pull to influence the strength of the connection.
For practical installation, let’s limit ![]() to 2 inches. Let’s set the embedment depth to 4 inches and use 5/8″ diameter screws. For reasons I haven’t been able to work out yet, the Simpson technical literature uses an effective embedment length significantly smaller than the nominal embedment length. Consulting the ESR, we get an effective embedment depth of 2.97 inches.
to 2 inches. Let’s set the embedment depth to 4 inches and use 5/8″ diameter screws. For reasons I haven’t been able to work out yet, the Simpson technical literature uses an effective embedment length significantly smaller than the nominal embedment length. Consulting the ESR, we get an effective embedment depth of 2.97 inches.
Doing the math gives us a basic concrete breakout strength of 1,069 lb/screw at a minimum spacing of 6 inches. Applying the factors (all 1, except for the parallel edge factor = 2 and the strength reduction factor, ![]() gives us an LRFD breakout strength of 1,496 lb/anchor.
gives us an LRFD breakout strength of 1,496 lb/anchor.
This is our ultimate capacity for overstrength loads. To calculate the basic shear force that will produce this overstrength load, we divide by 1.92 (based on an overstrength factor, ![]() and a redundancy factor,
and a redundancy factor, ![]() ) to get 778 lb/anchor LRFD.
) to get 778 lb/anchor LRFD.
Finally, we can factor this load to convert to ASD. Assuming only seismic loads, the LRFD factor is 1.0 and the ASD factor is 0.7, so we multiply by 0.7 to get 545 lb/anchor ASD.
At a spacing of 6 inches, this gives us a maximum anchorage capacity of 1,090 plf, which is equivalent to a ‘g’ mark in our standard Shear Wall Connections table.
Checking the other failure modes, the factored shear capacity of a 5/8″ concrete screw anchor is 3,360 lb/anchor (the overstrength reduction does not apply to this, because this is not a concrete-controlled capacity), and the factored pryout strength is calculated as follows:
![]()
![]() lb
lb
![]() in2
in2
![]() in2
in2
![]()
![]()
![]()
![]() for cracked concrete sections
for cracked concrete sections
![]()
![]() lb/screw
lb/screw
![]() lb/screw
lb/screw
Factoring this down in the same way as concrete breakout (![]() , dividing by 1.92 for overstrength, multiplying by 0.7 for LRFD to ASD factor conversion) gives us a factored pryout strength of 1,175 lb/screw. Concrete breakout at the parallel edge controls.
, dividing by 1.92 for overstrength, multiplying by 0.7 for LRFD to ASD factor conversion) gives us a factored pryout strength of 1,175 lb/screw. Concrete breakout at the parallel edge controls.
As a final check, the bolt capacity of a 5/8″ concrete screw anchor in a 2x SPF base plate is 1,764 lb/screw, so the concrete breakout strength is the final control.
Recent Posts
Categories
- Accessibility (2)
- Annotation Templates (1)
- Building Code (6)
- Calculation Templates (2)
- Civil Engineering (3)
- Derivations (8)
- Drafting Standards (18)
- Energy Code (1)
- Geotechnical Engineering (2)
- IT & Software Setup (5)
- Land Use Code (1)
- Product Knowledge (9)
- Production Tutorial (7)
- Research Notes (9)
- Research Tips (1)
- Revit Families (2)
- Revit Tips (5)
- Standard Operating Procedures (6)
- Stormwater (4)
- Structural Calculators (4)
- Structural Engineering (30)
- Structural General (11)
- Uncategorized (29)