Derivation: Pinned-Pinned Column with Load Applied at Arbitrary Location
Last updated November 18, 2022
By Ian Story
Position the load a distance b from the bottom and a from the top
The top and bottom of the beam will have different deflection equations.
Reactions
(1) ![]()
(2) ![]()
Bottom
(3) ![]()
(4) ![]()
(5) ![]()
Use moment-curvature relationship: ![]()
(6) ![]()
(7) ![]()
where:
(8) ![]()
Use general solution for column buckling differential equation. Set the final integration constant to zero due to boundary condition (![]() )
)
(9) ![]()
where:
(10) ![]()
Check solution works:
(11) ![]()
(12) ![]()
(13) ![]()
All the terms cancel out and we get 0 = 0, so this solution works
Top
(14) ![]()
(15) ![]()
Use moment-curvature relationship: ![]()
(16) ![]()
(17) ![]()
where:
(18) ![]()
Integrate twice, setting the final integration constant to zero due to boundary condition ![]()
(19) ![]()
Boundary Conditions
The moment for the bottom section at x = 0 is zero (pin connection), which gives us the following boundary condition:
(20) ![]()
The two sections meet at the point of load, which gives us three additional boundary conditions:
(21) 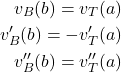
Solve for First Boundary Condition
(22) ![]()
Solve for Second Boundary Condition
(23) ![]()
(24) ![]()
(25) ![]()
(26) ![]()
where:
(27) ![]()
Solve for Third Boundary Condition
(28) ![]()
where:
(29) ![]()
(30) ![]()
(31) ![]()
(32) ![]()
Solve for Fourth Boundary Condition
(33) ![]()
where:
(34) ![]()
(35) ![]()
(36) ![]()
Equate and Collect Terms
(37) ![]()
(38) ![]()
Divide both sides by sin(kb)
(39) ![]()
(40) ![]()
(41) ![]()
Expand and Simplify
(42) ![]()
(43) ![]()
Cancel terms (note: ![]() , so
, so ![]() )
)
(44) ![]()
Multiply by ![]()
(45) ![]()
Multiply by ![]()
(46) ![]()
(47) ![]()
where:
(48) ![]()
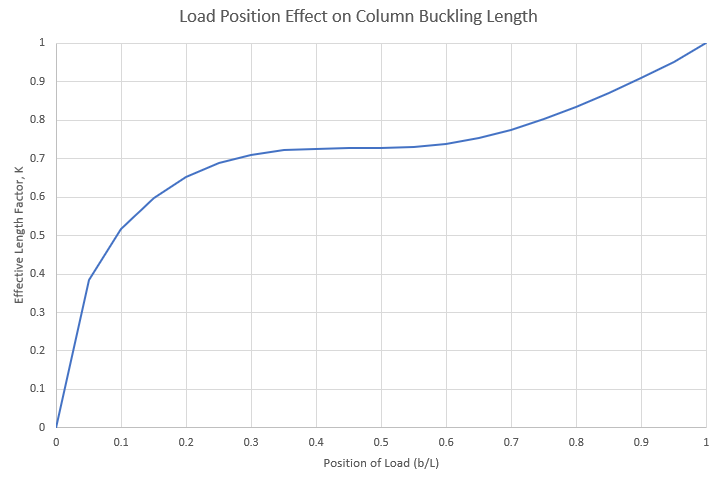
Graph to Find Values
This is a transcendental equation, so there is no algebraic solution. We will need to use a graphing utility or numeric solver to identify roots. Solving the above equation for a range of values gives the following table.
Effective length factors are calculated by converting to the standard column buckling format:
(49) ![]()
(50) ![]()
(51) ![]()
(52) ![]()
(53) ![]()
where:
(54) ![]()
| b/L | kb | Effective Length Factor (K) |
| 1.00 | 3.141 | 1.00 |
| 0.95 | 3.134 | 0.95 |
| 0.90 | 3.110 | 0.91 |
| 0.85 | 3.070 | 0.87 |
| 0.80 | 3.013 | 0.83 |
| 0.75 | 2.936 | 0.80 |
| 0.70 | 2.835 | 0.78 |
| 0.65 | 2.708 | 0.75 |
| 0.60 | 2.551 | 0.74 |
| 0.55 | 2.366 | 0.73 |
| 0.50 | 2.160 | 0.73 |
| 0.45 | 1.945 | 0.73 |
| 0.40 | 1.731 | 0.73 |
| 0.35 | 1.524 | 0.72 |
| 0.30 | 1.327 | 0.71 |
| 0.25 | 1.141 | 0.69 |
| 0.20 | 0.962 | 0.65 |
| 0.15 | 0.787 | 0.60 |
| 0.10 | 0.608 | 0.52 |
| 0.05 | 0.408 | 0.38 |
| 0.00 | 0.000 | 0.00 |
Recent Posts
Categories
- Accessibility (2)
- Annotation Templates (1)
- Building Code (6)
- Calculation Templates (2)
- Civil Engineering (3)
- Derivations (8)
- Drafting Standards (18)
- Energy Code (1)
- Geotechnical Engineering (2)
- IT & Software Setup (5)
- Land Use Code (1)
- Product Knowledge (9)
- Production Tutorial (7)
- Research Notes (9)
- Research Tips (1)
- Revit Families (2)
- Revit Tips (5)
- Standard Operating Procedures (6)
- Stormwater (4)
- Structural Calculators (4)
- Structural Engineering (30)
- Structural General (11)
- Uncategorized (29)