Retaining Walls – Resisting Sliding
Last updated April 4, 2025
By Ian Story
This article discusses the techniques and tricks available to resist sliding when designing a retaining wall.
Concrete retaining walls, ecology blocks, rockeries, and other common retaining wall designs need to resist the driving pressure of earth forces without tipping over and without sliding along their base. It has been our experience that sliding is often the controlling factor, especially for retaining walls with short heels (and on tight residential sites, it’s basically guaranteed that retaining walls will have a short heel). Sliding is often harder to design for than overturning. For overturning, you can increase the overturning resistance of a wall by extending the footing, which increases the moment arm of the resisting forces. But sliding resistance is typically controlled by friction, which is a function of the total weight bearing on the footing. There just aren’t many good ways to meaningfully increase a footing’s weight enough to make a difference.
Fundamentally, there are only four ways to increase the sliding resistance of a retaining wall:
- Friction
- Slab resistance
- Passive pressure (via a soil key)
- Tiebacks
Friction
A retaining wall’s first defense against sliding is friction. The available sliding resistance from friction is equal to the soil’s coefficient of friction (typically indicated by the character ![]() ) times the total unfactored dead load on the footing. IBC 1807.2.3 requires a minimum safety factor (resisting force / driving force) of 1.5 for static loads, which can be reduced to 1.1 for seismic loads. There are really only two levers here: you can increase the dead load or use a higher coefficient of friction.
) times the total unfactored dead load on the footing. IBC 1807.2.3 requires a minimum safety factor (resisting force / driving force) of 1.5 for static loads, which can be reduced to 1.1 for seismic loads. There are really only two levers here: you can increase the dead load or use a higher coefficient of friction.
There aren’t many good options available for increasing the dead weight. If space isn’t an issue, the best method is to use the backfill soil behind the retaining wall as a source of weight. You can do this by extending the heel (all of the soil above the heel counts as dead weight for resisting sliding) or by incorporating sheets of tensile reinforcement into the backfill and interlocking those sheets with the retaining wall (this technique is called a Mechanically Stabilized Earth retaining wall, and is a best practice for tall block-type retaining walls). The challenge with both of these techniques is that you need to overexcavate to install the footing, which defeats the purpose of using a retaining wall in the first place on a tight site.
The other option to increase the dead load is simply to pour more concrete. You can make the footing wider or thicker, which adds weight. But this is a very inefficient way to reach the goal and should generally be considered only if a small amount of additional sliding resistance is required.
The other way to look at increasing your wall’s friction resistance is to consider the coefficient of friction (![]() ) used. The coefficient of friction is a function of the underlying soil properties, and is typically presented in a geotechnical report or based on presumed values from IBC Table 1806.2. These values will typically be in the range of 0.3 to 0.4. General consensus on engineering forums seems to be that these values are too low and produce wildly overconservative designs if a further 1.5 safety factor is then applied (see here and here).
) used. The coefficient of friction is a function of the underlying soil properties, and is typically presented in a geotechnical report or based on presumed values from IBC Table 1806.2. These values will typically be in the range of 0.3 to 0.4. General consensus on engineering forums seems to be that these values are too low and produce wildly overconservative designs if a further 1.5 safety factor is then applied (see here and here).
After further research into this topic, here is my current best understanding of soil friction:
- The nominal soil friction coefficient is equal to
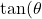 , where
, where 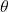 is the friction angle of the slip plane being considered.
is the friction angle of the slip plane being considered. - For soil to soil interfaces,
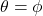 , where
, where 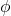 is the weaker soil’s internal friction angle. Where slip failures occur in a weaker stratum away from the footing, this would be the value to use.
is the weaker soil’s internal friction angle. Where slip failures occur in a weaker stratum away from the footing, this would be the value to use. - For concrete to soil interfaces,
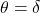 , where
, where 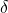 is the interface friction angle between the concrete and soil. Of key interest is the ratio between this interface friction angle and the soil’s internal friction angle (
is the interface friction angle between the concrete and soil. Of key interest is the ratio between this interface friction angle and the soil’s internal friction angle (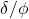 ).
).
- For coulomb analyses involving the interface between backfill soil and formed concrete faces (the back of the retaining wall), the typical value for
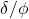 is 2/3.
is 2/3. - Friction coefficient calculations for retaining wall footings are typically given based on a
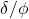 value of 2/3 or 0.7. But it is unclear if these include a factor of safety (using these numbers produces approximately a 1.5 factor of safety compared to using
value of 2/3 or 0.7. But it is unclear if these include a factor of safety (using these numbers produces approximately a 1.5 factor of safety compared to using 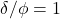 ).
). - It could credibly be argued that
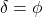 in cases where the footing is cast directly against earth and there is significant roughness to create interlock with the soils. Research papers we reviewed generally showed values of around 2/3 for smooth concrete and 0.95 to 1.0 for rough concrete.
in cases where the footing is cast directly against earth and there is significant roughness to create interlock with the soils. Research papers we reviewed generally showed values of around 2/3 for smooth concrete and 0.95 to 1.0 for rough concrete.
- For coulomb analyses involving the interface between backfill soil and formed concrete faces (the back of the retaining wall), the typical value for
- Based on the available research, we are comfortable assuming the nominal soil friction coefficient for the bottom of footings cast directly against soil is approximately equal to
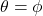 , where
, where 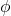 is the internal friction angle of the weakest soil stratum below the footing.
is the internal friction angle of the weakest soil stratum below the footing. - For design purposes, a safety factor of 1.5 is applied to this nominal soil friction coefficient. This is likely the value that is typically reported in a geotechnical report and in the presumed friction coefficients in the IBC. For illustration, a silty sand with
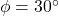 would have a nominal friction coefficient of
would have a nominal friction coefficient of 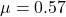 , which when divided by 1.5 gives the more typical value of 0.38.
, which when divided by 1.5 gives the more typical value of 0.38. - Sliding failures are rarely catastrophic failures. As the wall slides away from the soil, the soil pressure will decrease. Over time the soil may continue to creep and ratchet the wall forward. While this will eventually produce unacceptable service conditions, it is unlikely to become a life safety issue before the damage is observable.
Based on this understanding, our standard practice for designing retaining walls is to use nominal values for the input to retaining wall design programs (like Enercalc), which will then create the necessary factor of safety by ensuring that the available resisting forces are at least 1.5 times higher than the driving forces. As long as the geotechnical report specifies that their coefficient of friction values include a factor of safety, you can mark those values up to nominal values before inputting them into design software. Doing so avoids double-counting the 1.5 safety factor and produces designs much more in line with retaining wall rules of thumb and contractor expectations.
Sources
- Eng-Tips Coefficient of Friction b/w Concrete and Soil
- Eng-Tips Soil-Foundation Friction Angle (Friction Angle for Foundation Surface)
- Eng-Tips Sliding Stability, Coefficient of friction given soils angle of internal friction
- Factors of Safety and Reliability in Geotechnical Engineering, Duncan
- Determination of soil shear properties on a soil to concrete interface using a direct shear box apparatus, Ilori (their testing appears to indicate that the interface friction is higher than the internal soil friction)
- Evaluation of the friction angle soil-wall and the roughness of the surface of contact, Ferreira (provides a literature comparison table for the relationship between
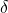 and
and 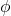 for smooth and rough concrete)
for smooth and rough concrete) - Sand–concrete interface response: The role of surface texture and confinement conditions, Nadrelli (tests concrete-sand interface and finds
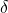 and
and 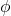 values north of 0.95)
values north of 0.95)
Recent Posts
Categories
- Accessibility (2)
- Annotation Templates (1)
- Building Code (6)
- Calculation Templates (2)
- Civil Engineering (3)
- Derivations (8)
- Drafting Standards (18)
- Energy Code (1)
- Geotechnical Engineering (2)
- IT & Software Setup (5)
- Land Use Code (1)
- Product Knowledge (9)
- Production Tutorial (7)
- Research Notes (9)
- Research Tips (1)
- Revit Families (2)
- Revit Tips (5)
- Standard Operating Procedures (6)
- Stormwater (4)
- Structural Calculators (4)
- Structural Engineering (30)
- Structural General (11)
- Uncategorized (29)