Structural Screws

Last updated February 22, 2024
By Ian Story

There are many different brands and products of structural screws designed for fastening wood members (SDS screws, LedgerLOK, HeadLOK, timberLOK). These structural screws are typically designed to replace lag screws without requiring pre-drilling, resulting in significant cost savings for labor. Most of these products have a similar diameter of slightly under 1/4.” This is likely around the limit for what can be installed without splitting the wood, and it also plays into many favorable NDS exemptions for fasteners under 1/4″ diameter.

Most of these screws include load test data in the form of ESR reports. These reports potentially allow you to use a higher capacity than what is possible under the NDS equations for generic fasteners, but they also come with much more restrictive spacing and edge clearance requirements than the NDS. Applying these additional requirements may result in a lower overall connection capacity for space-limited connections.

This article will address using structural screws as generic dowel-type fasteners under the NDS.

Specification

For the remainder of this article, I will assume we are working with one of two types of Structural Screws meeting the following minimum specifications:

PropertyLight Structural ScrewHeavy Structural Screw
Unthreaded shank diameter, D0.189 in0.220 in
Bending yield stress, Fyb160,000 psi160,000 psi

Light Structural Screws include TimberLOK and HeadLOK, SDWH, SDWS19, RSS5/16

Heavy Structural Screws include LederLOK, SDS, SDW, SDWS22, RSS3/8

Calculations – Light Structural Screw

All calculations are per NDS 2018 Table 12.3.1A

SPF Lumber: 2x side member, main member at least 1 3/4″


D = 0.189\text{ in}
F_{yb} = 160,000\text{ psi}
R_d = K_d = 10D + 0.5 = 10(0.189) +0.5 = 2.39}
R_e = F_{em}/F_{es} = 1
F_{em} = 3,350\text{ psi}
F_{es} = 3,350\text{ psi}
R_e = F_{em}/F_{es} = 1
R_t = l_m/l_s = 1.167
l_m = 1.75\text{ in}
l_s = 1.5\text{ in}

k_1 = \cfrac{\sqrt{R_e+ 2R_e^2(1 + R_t + R_t^2) + R_t^2R_e^3} - R_e(1 + R_t)}{1 + R_e}

k_1 = \cfrac{\sqrt{1+ 2*1^2(1 + 1.167+ 1.167^2) + 1.167^2*1^3} - 1(1 + 1.167)}{1 + 1}

k_1 = 0.451

k_2 = -1 + \sqrt{2(1+R_e)+\cfrac{2F_{yb}(1+2R_e)D^2}{3F_{em}l_m^2}}

k_2 = -1 + \sqrt{2(1+1)+\cfrac{2(160,000)(1+2*1)(0.189)^2}{3(3,350)(1.75)^2}} = 1.261

k_3 = -1 + \sqrt{\cfrac{2(1+R_e)}{R_e}+\cfrac{2F_{yb}(2+R_e)D^2}{3F_{em}l_s^2}}

k_3 = -1 + \sqrt{\cfrac{2(1+1)}{1}+\cfrac{2(160,000)(2+1)(0.189)^2}{3(3,350)(1.5)^2}} = 1.349

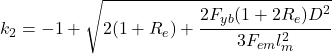
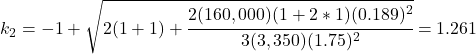
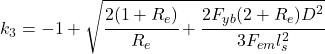
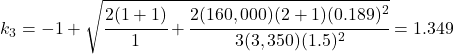
Yield Mode Calculations:

I_m = \cfrac{Dl_mF_{em}}{R_d} = \cfrac{(0.189\text{ in})(1.75\text{ in})(3,350\text{psi})}{2.39} = 464\text{ lb}

I_s = \cfrac{Dl_sF_{es}}{R_d} = \cfrac{(0.189\text{ in})(1.5\text{ in})(3,350\text{psi})}{2.39} = 397\text{ lb}

II = \cfrac{k_1Dl_sF_{es}}{R_d} = \cfrac{(0.451)(0.189\text{ in})(1.5\text{ in})(3,350\text{psi})}{2.39} = 179\text{ lb}

III_m = \cfrac{k_2Dl_mF_{em}}{(1+2R_e)R_d} = \cfrac{(1.261)(0.189\text{ in})(1.75\text{ in})(3,350\text{psi})}{(1+2*1)2.39} = 194\text{ lb}

III_s = \cfrac{k_3Dl_sF_{em}}{(1+2R_e)R_d} = \cfrac{(1.349)(0.189\text{ in})(1.5\text{ in})(3,350\text{psi})}{(1+2*1)2.39} = 179\text{ lb}

IV = \cfrac{D^2}{R_d}\sqrt{\cfrac{2F_{em}F_{yb}}{3(1+R_e)}} = \cfrac{(0.189\text{ in})^2}{2.39}\sqrt{\cfrac{2(3,350\text{psi})(160,000\text{psi})}{3(1+1)}} = 200\text{ lb}

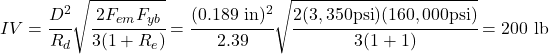
Discussion

The NDS calculated capacity for a Light Structural Screw is 179 pounds. Compare this to the tested capacity of 240 pounds for a TimberLOK screw (ESR-1078). However, the minimum edge distance for the NDS screw is 1.5D (0.29″) compared to the tested 1.75″; the minimum spacing between rows for the NDS screw is 1.5D (0.29″) compared to the tested 1.38″; and the minimum spacing between fasteners in a row is 4D (0.76″) compared to the tested 4″. For a fastener with limited space, such as a short 2×4, you can theoretically fit roughly 25x as many screws into a given area using the NDS calcs (5 rows @ 15 fasteners per foot for NDS vs 1 row @ 3 fasteners per foot). Practically, the limit is smaller due to concerns about installation and splitting the wood, but the point stands: NDS generic screws can achieve a higher capacity per unit of length or area than the tested connectors can.