Calculations: Torsion in Orthotropic Rectangular Beams
Last updated June 27, 2022
By Ian Story
The following equations come from Lekhnitskii, S.G. 1981. Theory of elasticity of an anisotropic body (page 285).
(1) ![]()
(2) 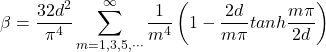
(3) 
(4) 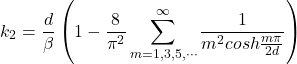
(5) ![]()
(6) ![]()
An excel calculator with Lambda functions to solve for each of these parameters as a function of d is available here: Torsion Factors for Orthotropic Rectangular Sections.xlsx
Input Values
Shear modulus ratios (g) can be found in research by Hindman: Hindman et al. 2000. Orthotropic Behavior of Lumber Composite Materials. Trus Joist publishes shear modulus (G) values in their product data guides: LSL Product Data. Generally, it looks like G (in the principal plane) for LSL members is approximately equal to E divided by 16.
Recent Posts
Categories
- Accessibility (2)
- Annotation Templates (1)
- Building Code (6)
- Calculation Templates (2)
- Civil Engineering (3)
- Derivations (8)
- Drafting Standards (18)
- Energy Code (1)
- Geotechnical Engineering (2)
- IT & Software Setup (5)
- Land Use Code (1)
- Product Knowledge (9)
- Production Tutorial (7)
- Research Notes (9)
- Research Tips (1)
- Revit Families (2)
- Revit Tips (5)
- Standard Operating Procedures (6)
- Stormwater (4)
- Structural Calculators (4)
- Structural Engineering (30)
- Structural General (11)
- Uncategorized (29)