Torsion in Wood Beams
Last updated September 9, 2022
By Ian Story
Generally, engineering standards and best practices recommend avoiding loading wood beams in torsion. However, there are situations where minor torsion loads are unavoidable, or where introducing limited amounts of torsion can significantly simplify connection details. Rather than avoid torsion entirely, we have taken the time to understand its limits so we can use it beneficially in small amounts where called for. The most common situations I see where torsion come up in residential wood design are for side-mounted joist hangers and for guardrail connections – the latter is a very common condition, and most of the following research came about in the search for better guardrail attachment details.
Shear Stresses Due to Torsion
The first thing to note is that torsion in a member produces shear stress. When you apply a torque to twist a beam, each transverse “slice” of the beam wants to rotate relative to the next slice, and this rotation is resisted by shear stresses through the thickness of the beam. To maintain shear compatibility, these tangential shear stresses will also produce corresponding longitudinal shear stresses along the length of the beam, tending to split the beam along its outside face. Since wood is significantly stronger in shear across the grain than parallel to the grain, we can safely ignore the cross-grain shear and concentrate just on the shear parallel to the grain.
Any introductory mechanics of materials course will cover how to calculate shear stresses for a circular shaft. But the picture gets much more complicated when working with a rectangular section. Generally, shear stresses will increase as you get further out from the center of rotation. In a rectangular section, these shear stresses will be at a maximum at the middle of the wide faces of the beam. The shear stresses will decrease to zero at the corners and will rise to a local maximum at the middle of the narrow faces of the beam. The derivation of this shear distribution is beyond the scope of this article – see the references section at the bottom for further reading sources.
Another challenge to calculating torsion in wood beams is the material properties of wood itself. Wood is a highly anisotropic material (meaning that its engineering properties are different depending on what direction you are considering). We already established that we can safely disregard the cross-grain direction for this analysis. But some wood members also vary in strength and stiffness depending on whether you are considering the wide or narrow face of the beam. Generally, it’s reasonable to treat these two planes as identical for solid sawn lumber, but engineered lumber (LVL, PSL, and LSL) does vary significantly between these two planes, and we need to take those differences into account to conduct a complete analysis.
For determining the distribution of shear forces in the member, we need to consider the relative stiffness of each of the two tangential directions. This stiffness is described by the Shear Modulus, denoted uppercase G (psi). Specifically, we need to know the ratio between the Shear Modulus parallel to the wide face of the beam and the Shear Modulus parallel to the narrow face of the beam, denoted by lowercase ![]() . For materials that do not vary appreciably between these two places, you can set g=1.
. For materials that do not vary appreciably between these two places, you can set g=1.
Shear Stress Equations
The following equations provide the maximum shear stress at each face of a wood beam. The equations come from Lekhnitskii (see references below) and are based on converging infinite series. I am presenting the equations here for completeness. For practical application, you can use the calculation widget below or the following Excel spreadsheet: Torsion Factors for Orthotropic Rectangular Sections.xlsx
(1) ![]()
(2) 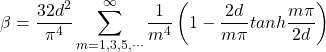
(3) 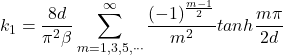
(4) 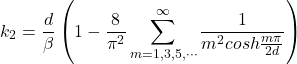
(5) ![]()
(6) ![]()
where:
(7) 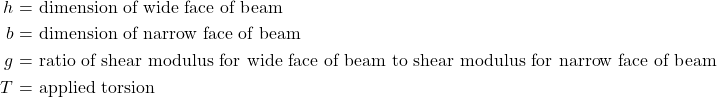
Calculator
Allowable Shear Stresses
Per the AITC Timber Construction Manual, the recommended allowable shear due to torsion (Fvt) is 2/3 of the allowable longitudinal shear.
For glulam beams, the allowable shear for torsion applications must be further reduced by a torsional shear reduction factor (Cvt = 0.72). Because shear will be critical in the wide face, use Fvx for the base shear.
For engineered lumber, you need to check both faces separately (this is most critical for LSL beams, because allowable shear for the narrow face is much smaller than for the wide face).
Typical Nominal Shear Stresses (Fvt)
| Wide Face | Narrow Face | |
| Douglas Fir | 113 psi | 113 psi |
| SPF | 90 psi | 90 psi |
| Glulam | 127 psi | 127 psi |
| LSL | 336 psi | 100 psi |
| LVL | 190 psi | 127 psi |
| PSL | 153 psi | 127 psi |
References
- Roark’s Formulas for Stress and Strain, p. 401. Provides formulas for maximum shear stress due to torsion for various sections (assuming isotropic materials).
- Lekhnitski. Theory of Elasticity of an Anistropic Body, p. 283. Provides formulas to calculate torsion constants for orthotropic materials.
- Siller, T.S. 2000. Evaluation of the torsion test as a method to determine the shear strength of structural composite lumber. Thesis exploring torsion as a testing method to establish ultimate shear stresses of structural composite lumber. Includes test data on LVL, PSL, and LSL members.
- Hindman. 2000. Orthotropic behavior of lumber composite materials. Thesis determining the directional Elastic Modulus and Shear Modulus values for structural composite lumber. Includes test data on LVL, PSL, and LSL members.
- US Forest Products Laboratory. 2010. Wood handbook: wood as an engineering material. Wood design handbook that includes limited information on torsion (note: the formula for shear stresses in a rectangular beam looks to have significant errors).
- AITC Timber Construction Manual, 6th Edition, p. 130. Provides recommended allowable stresses for shear due to torsion, in addition to worked examples.
- Faherty, Williamson. 1999. Wood Engineering and Construction Handbook, p. 4.17. Basic treatment of torsion in beams. Includes a simplified formula for shear stresses and a discussion of radial tensile stress for glulam beams. Note: this book is only available in hard copy – we have a copy in the office.
Recent Posts
Categories
- Accessibility (2)
- Annotation Templates (1)
- Building Code (6)
- Calculation Templates (2)
- Civil Engineering (3)
- Derivations (8)
- Drafting Standards (18)
- Energy Code (1)
- Geotechnical Engineering (2)
- IT & Software Setup (5)
- Land Use Code (1)
- Product Knowledge (9)
- Production Tutorial (7)
- Research Notes (9)
- Research Tips (1)
- Revit Families (2)
- Revit Tips (5)
- Standard Operating Procedures (6)
- Stormwater (4)
- Structural Calculators (4)
- Structural Engineering (30)
- Structural General (11)
- Uncategorized (29)